Robotik 1

Oct 15, 2018

1. Vorlesung

Link zu den Folien der ersten Vorlesung.

Organisation

Institut für Anthropomatik und Robotik (IAR)

Hochperformante humanoide Technologien (H²T)

humanoids.de

Übung findet alle 14 Tage statt.

Videos von WS17/18 auf DIVA: DIVA Videos

Coole Videos vom Lehrstuhl

Ilias-Kurs

Schriftliche Klausur: 1 Stunde lang

Es waren in der ersten Vorlesung sehr viele Studis da:

Literatur

Robotics: Control, Sensing, Vision, and Intelligence; Fu, Gonzalez, Lee
Springer Handbook of Robotics; Editors: Bruno Siciliano, Oussama Khatib http://handbookofrobotics.org/
Artificial Intelligence - A Modern Approach, 3rd. Ed.; Russel, Norvig
Robotics, Vision and Control: Fundamental Algorithms in Matlab, Peter Corke Wird in den Übungen verwendet werden
Modern Robotics: Mechanics, Planning and Control, Kevin M. Lynch, Frank C. Park

Folien sollten eigentlich umfangreich genug sein. Auf notwendige Zusatzliteratur wird hingewiesen.

Software

Motivation

Humanoide Roboter bauen. Fokus bei H²T auf Händen und Lernen. Armar-Roboter. Einer hat auch Beine. Roboterhände und Prothesen.

“Laufen ist nur die Transition” zwischen auf einem Bein stehen, auf zwei Beinen stehen und dann auf dem anderen Bein stehen. H²T hat eine Taxonomie erstellt, in der nach Kontaktpunkten mit Boden und Wänden und Größe dieser Kontaktpunkte alle Körperposen des Menschen eingeordnet werden.

Das ist mit Aufnahmen von Menschen geschehen -> größte, öffentlich verfügbare Bewegungsdatenbank der Welt: https://motion-database.humanoids.kit.edu/

Wenn man die Posen der Menschen nach der Taxonomie klassifiziert, dann kann man die Handlungen und Bewegungen als Transitionsgraph zwischen diesen darstellen.

“Motion to Language”: Bewegungsaufnahme in rekurrentes Netzwerk -> Ausgabe sind Beschreibungstexte. Es wurde danach sogar anders herum gemacht. Eingabe war der Beschreibungstext und Ausgabe dann eine generierte Bewegung.

Wenn man die Taxonomie der Posen als Alphabet sieht, dann kann man die Idee von n-grams aus der Spracherkennung verwenden, um Bewegungen vorherzusagen bzw. zu planen.

Definition Roboter? Hat sich über die Zeit gewandelt. Lange und begeisterungsreiche Historie. Auch autonome Autos sind Roboter.

Generation ab 1960: Programmierbare Manipulatoren (geringe Rechenleistung, Punkt-zu-Punkt-Programmierung und kaum Sensoren)
Generation ab 1980: Adaptive Roboter (Sensoren zur Anpassung an Umwelt, Programmiersprache VAL, geringe Intelligenz)
Generation ab heute: Autonome Roboter (hohe Rechenleistung, spezialisiert auf Aufgaben, autonomes Handeln)
Generation ab Zukunft: Humanoide/AI Roboter (hohe Flexibilität bzgl. Umwelt, Lernen und Anpassen, Selbstreflexion?, Emotion?)

Teilbereiche:

Sensorik (Technologien, Signalverarbeitung)
Aktorik (Antriebe, Kinematiken, Gelenktypen)
Modellierung (Roboter, Umwelt, Sensorik)
Schnittstellen (Programmierung, Bedienung, Direkte Kommunikation)
Verbunden durch: Datenvearbeitung (KI, ML, Wahrnehmung, Symbolische Planung, Manipulation, Architekturen, Regeln und Steuern, Sensordatenfusion)

Industrieroboter: Wenige DOF, Art der Steuerung (Point-To-Point, kontinuierlicher Pfad, Adaptive, Teleoperativ), mechanische Struktur (SCARA, parallel)

Serviceroboter: halb- oder vollautonom, nützliche Dienste für den Menschen (nicht Industrie)

Personal Robot: Roboter, der menschliches Verhalten nachahmt im Bereich der Bewegung, Intelligenz und Kommunikation.

2. Vorlesung

“Roboter, bring mir einen Saft aus dem Kühlschrank.” -> Motivation für Koordinatensystem (Punkte und Rotationen in 3d beschreiben)

Generell sind drei Bereiche der Mechanik interessant für Robotik:

Statik: Behandelt Kräfte und Momente, die sich auf den ruhenden Mechanismus auswirken. Steifigkeit
Dynamik: Betrachtet Kraft und Moment, welche durch Beschleunigung/Bewegung und zusätzlicher Last entstehen
Kinematik: Analysiert die Geometrie eines Manipulators oder Roboters. Position

Als Endeffektor bezeichnet man beim humanoiden Roboter zum Beispiel die Hände, Greifer oder aufgesetzte Werkzeuge.

Ein Roboter hat Gelenke (Ellenbogengelenk) und Glieder (z. B. Unterarm). Deren Zusammenhang kann in einer Kinematischen Kette dargestellt werden. Repräsentiert als Graph. Kanten sind Glieder, Knoten sind Gelenke.

Freiheitsgrade oder Degrees of Freedom (DoF). Ist die Anzahl an Parametern, die nötig sind um die räumliche Lage, eines Objektes oder Mechanismus zu beschreiben. Zum Beispiel hat ein Punkt auf einer 2d-Ebene zwei Freiheitsgrade. Und ein Starrkörper hat durch seine Position und Orientierung um 3D-Raum 6 DoF.

Starrkörperbewegung (zum Beispiel Staubsaugerroboter, aber kein Tintenfisch):

Die Distanz zweier Punkte bleibt erhalten (vgl. mit einem Schwamm)
Die Orientierung des Körpers bleibt gleich (rechtsdrehendes Koordinatensystem bleibt)

SO(3)

Spezielle Orthogonale Gruppe im R³: SO(3)

“Volumen im Raum bleibt erhalten”: $ det(A) = 1 $
“Die Transponierte ist die Inverse”: $ R^{T} R = I => R^{T} = R^{-1} $

Eine 3x3-Matrix, die diese beiden Anforderungen erfüllt, kann als SO(3) für Rotationen von Starrkörpern verwendet werden.

SE(3)

Spezielle Euklidische Gruppe im R³: SE(3)

Wird für die Starrkörperbewegung verwendet.

Es handelt sich um eine Zusammensetzung einer Rotation R aus SO(3) und einem Translationsvektor t (Spaltenvektor 3x1):

$\begin{bmatrix} SO(3)_{1,1} & SO(3)_{1,2} & SO(3)_{1,3} & t_{1,1} \\ SO(3)_{2,1} & SO(3)_{2,2} & SO(3)_{2,3} & t_{2,1} \\ SO(3)_{3,1} & SO(3)_{3,2} & SO(3)_{3,3} & t_{3,1} \end{bmatrix}$

Euklidischer Raum

Vektorraum R³ mit dem Standardskalarprodukt, also: Wenn ein Punkt auf einer Strecke zwischen zwei Punkte liegt, dann kann jeder Punkte auf der Linie durch eine Linearkombination der beiden Punkte dargestellt werden.

Punkt c auf der Strecke zwischen a und b: $ c = t * a + (1-t) * b $, wobei t den Einfluss von a reguliert (sollte zwischen 0 und 1 liegen).

Ein Punkt im euklidischen Koordinatensystem kann durch eine Linearkombination der Basisvektoren (Achsen $e_x, e_y, e_z$) repräsentiert werden. “3 Schritte die X-Achse entlang, -1 Schritt die Y-Achse und 2 die Z-Achse hoch.”

Die Basisvektoren sind orthogonal zueinander und normalisiert (Länge ist 1). Daher spricht man von einem orthonormalen Koordinatensystem.

Konvention: Rechtsdrehende Koordinatensysteme werden benutzt (Rechter Daumen der Hand zeigt nach oben, die Finger geben die Drehrichtung an)

Rechte Hand Regel: Rechte Hand Daumen nach rechts ist die X-Achse, Zeigefinger Y und Mittelfinger Z. Z-Achse soll nach oben zeigen.

Es gibt folgende Koordinatensysteme:

Basiskoordinatensystem (BKS): Steht in der Ecke vom Raum
Objektkoordinatensystem (OKS): Für ein Objekt zum Interagieren
Sensorkoordinatensystem (SKS): Für Sensoren (Kameras)
Endeffektorkoordinatensystem (EKS): Für Greifer, Hand oder ähnliches

Lineare Abbildungen $\phi: \mathbb{R}^3 \rightarrow \mathbb{R}^3$ , die R³ auf sich selbst abbilden heißten Endomorphismen. Man repräsentiert sie mit quadratischen Matrizen. Zum Beispiel beschreibt folgende Formel ausmultipliziert eine Matrix, die einen Basiswechsel durchführt (also von einem Koordinatensystem in ein anderes): $ (e_x e_y e_z) (e’_x e’_y e’_z)^{-1} $

Ein bijektiver Endomorphismus heißt Isomorphismus. (Umkehrbarkeit!)

Interessante Eigenschaften von Isomorphismen:

Winkelerhaltend: Skalierung, Rotation
Längenerhaltend: Rotation
Händigkeitserhaltend: Rotation erhält rechtshändiges Koordinatensystem

Rotationsmatrix

SO(3) ist ein Isomorphismus mit allen drei Eigenschaften. SO(3) enthält alle möglichen Rotationen um willkürlich durch den Ursprung gelegte Achsen und ist nicht kommutativ (keine abelsche Gruppe).

Wichtig für die Robotik: Objektpose und mit Verkettung mit Translation kann die Transformation zwischen zwei Gelenkachsen dargestellt werden. Dafür benötigen wir folgenden affinen Isomorphismus (nicht linear):

$\phi ( \cdot ) = R x + t, \space x, t \in \mathbb{R}^3, \space R \in SO(3)$

In 2d:

$\begin{bmatrix} cos \alpha & -sin \alpha \\ sin \alpha & cos \alpha \end{bmatrix}$

Test: Handelt es sich um eine Rotationsmatrix?

Antwort: Wenn $det(A) = 1$ und $R^{T} R = I$

Was machen, wenn man nicht um den Ursprung rotieren will? Dann verschiebt man vor der Rotation die Ebene über den Ursprung und schiebt sie dann wieder zurück. -> Das ist als affine Transformation darstellbar.

In 3d:

Für jede Achse gibt es eine Rotationsmatrix. Bei einer Rotation um die Z-Achse werden nur die Punkte im X-Y-Raum rotiert usw.

$R_{x, \alpha} = \begin{bmatrix} 1 & 0 & 0 \\ 0 & cos \alpha & -sin \alpha \\ 0 & sin \alpha & cos \alpha \end{bmatrix}$ $R_{y, \alpha} = \begin{bmatrix} cos \alpha & 0 & sin \alpha \\ 0 & 1 & 0 \\ -sin \alpha & 0 & cos \alpha \end{bmatrix}$ $R_{z, \alpha} = \begin{bmatrix} cos \alpha & -sin \alpha & 0 \\ sin \alpha & cos \alpha & 0 \\ 0 & 0 & 1 \end{bmatrix}$

Die inverse Rotationsmatrix entspricht der transponierten (Spiegelung über die Diagonale).

Verkettung von Rotationen: Man kann die Verkettung entweder von innen nach außen oder andersherum ausmultiplizieren.

Von rechts nach links (innen nach außen): globale Achsen, z. B. Roll-Pitch-Yaw (x-y-z)
Von links nach rechts (außen nach innen): lokale Achsen, z, x’, z’’

Probleme mit Rotationsmatrizen:

Redundanz: 27 Werte für 3 DoF (3 3x3-Matrizen für Rotation eines 3D-Punktes)
Ungültige Rotationsmatrizen: Problematisch für Machine Learning

Eulerwinkel

Drei Rotationen um drei willkürliche Achsen können jede Rotation beschreiben. Euler-Konvention der Achsen z, x’, z’‘. Die Winkel $\alpha, \beta und \gamma$ sind die Eulerwinkel. Sie beschreiben die Rotationsmatrix.

Diese ergibt sich, wenn man folgende Rotationsmatrizen von links nach rechts multipliziert: $R_{z, \alpha} R_{x', \beta} R_{z'', \gamma}$

Es sind 12 verschiedene Abfolgen für die Rotationsmatrizen möglich: z-x-z, x-y-x, … \ Diese kann man wiederum global oder lokal drehen -> 24 Möglichkeiten

Euler-Konvention ist x-y-z. Man nennt sie auch:

Rotation um x-Achse des BKS um alpha: Roll
Rotation um y-Achse des BKS um beta: Nick/Pitch
Rotation um z-Achse des BKS um gamma: Gier/Yaw

$R = R_z(\gamma) R_y(\beta) R_x(\gamma)$

Eulerwinkel sind aussagekräftiger und kompakter als Rotationsmatrizen.

Nachteile sind, dass Drehungen nicht eindeutig sind und sie sind nicht kontinuierlich. Letzteres heißt, dass eine stetige Interpolation zwischen zwei Eulerwinkeln nicht möglich ist. Des weiteren haben Eulerwinkel den Gimbal Lock. Gimbal (kardanische Lagerung) wird zum Beispiel in einem Gyroskop verwendet. Das bedeutet, dass es Rotationen gibt, die zwei Achsen voneinander abhängig machen, wodurch ein Freiheitsgrad verloren geht. Zum Beispiel für: $\beta = - {\pi \over 2} $

3. Vorlesung

=> Bei allen 3x3-Darstellungen fehlt die Translation, die man gesondert bearbeiten muss. Daher nutzt man affine Transformationen (aus der Geometrie), um den euklidischen Raum zu erweitern. Aus 3D-Koordinaten werden dann die 4D-Koordinaten namens homogene Koordinaten.

$a = (a_x, a_y, a_z, h)^T$ mit $h \in {0, 1}$

Homogene 4x4-Matrix

$T = \begin{bmatrix} A & t
o^T & 1 \end{bmatrix}$

mit A ist aus SO(3) und t ein Translationsvektor.

Wenn man den Ortsvektor $p_{OKS}$ im BKS darstellen möchte, dann geht das wie folgt: $p_{BKS} = T * p_{BKS}$ mit T …

$T = \begin{bmatrix} n_x & o_x & a_x & u_x \\ n_y & o_y & a_y & u_y \\ n_z & o_z & a_z & u_z \\ 0 & 0 & 0 & 1 \end{bmatrix} = \begin{bmatrix} n & o & a & u \\ 0 & 0 & 0 & 1\end{bmatrix}$

n: Ursprung des OKS n,o,a: Einheitsvektoren des OKS

Dort, wo eine 1 in der Diagonalen steht. Wo wird rotiert? Das soll man aus einer Rotationsmatrik lesen können.

Homogene Matrix

Homogene 4x4-Matrix: Repräsentiert Rotation und Translation in einer Matrix. Der Eintrag unten rechts ist der Skalierungsfaktor, bleibt aber in der Robotik immer eine 1. Die drei übrigen Einträge der Matrix haben auch Bedeutung für die Perspektive, sind aber bei uns immer Nullen.

Invertierung

Die SO(3) kann einfach transponiert werden. Die letzte Zeile bleibt gleich. Nur die rechte Spalte ist besonders, es gibt aber eine geschlossene Form.

$\begin{bmatrix} SO(3)^T & & & -n^{T} u \\ & & & -o^{T} u \\ & & & -a^{T} u \\ 0 & 0 & 0 & 1 \end{bmatrix}$

Eine homogene Matrix enthält 12 (4 x 3 n,o,a,u) nicht triviale Kenngrößen. Im Gegensatz zu den 6 notwendigen: $x, y, z, \alpha, \beta, \gamma$.
Redundanz wegen Orthogonalität ($RR^T = I$)
Drehachsen und Drehreihenfolge sind implizit enthalten

Lagebeschreibung 4x4 eines Objektes obj im Koordinatensystem KS: $\vphantom{\mathbf{C}}^{KS} \mathbf{C}^{}_{obj}$

Verkettete Lagebeschreibungen werden von links nach rechts multipliziert.

Man kann “kürzen”: $\vphantom{\mathbf{H}}^{BKS} \mathbf{H}^{}_{B} = \vphantom{\mathbf{H}}^{BKS} \mathbf{H}^{}_{A} \cdot \vphantom{\mathbf{H}}^{A} \mathbf{H}^{}_{B}$

Die homogene Matrix macht die Drehungen jedoch weiterhin über die Rotationsmatrix, daher hat sie auch die gleichen Nachteile.

Quaternionen

https://eater.net/quaternions/video/intro

https://eater.net/quaternions/video/doublecover

Quaternionen sind eine Erweiterung der Komplexen Zahlen von Hamilton (Dublin). “Hyperkomplexe Zahlen” $\mathbb{H} = \mathbb{C} + \mathbb{C}_j$ mit $j^2 = -1$ und $i \cdot j = -j \cdot i$.

Ein Quaternion $q \in \mathbb{H}$ hat folgende Form: $q = (a, \boldsymbol{u}) = a + u_1 \cdot i + u_2 \cdot j + u_3 \cdot k$ mit $k = i \cdot j$.

Regeln

Hamilton Regeln:

$i^2 = j^2 = k^2 = -1$
$ij = +k, \space jk = +i, \space ki = +i$
$ji = -k, \space kj = -i, \space ik = -j$

Der Koeffizient a wird als Realteil bezeichnet. Imaginärteil ist der Name von u. Hamilton hat alle Quaternionen mit einem Realteil von Null als Vektoren bezeichnet.

Rechenregeln für zwei Quaternionen q und r: $q = (a, u_1, u_2, u_3)^T und \space r = (b, v_1, v_2, v_3)^T$

Addition: $q + r = (a + b, u_1 + v_1, u_2 + v_2, u_3 + v_3)^T$

Skalarprodukt: $ \langle q | r \rangle = a \cdot b + u_1 \cdot v_1 + u_2 \cdot v_2 + u_3 \cdot v_3 $

Multiplikation: Ausmultiplizieren, aber nicht kommutativ!

Konjugation: Wenn Quaternion $q = (a, \boldsymbol{u} )^T $, dann ist die Konjugation $ q^{*} = (a, - \boldsymbol{u} ) $

Norm: $\bigl| q \bigl| = \sqrt {q \cdot q^*} = \sqrt {q^* \cdot q} = \sqrt {a^2 + {u_1}^2 + {u_2}^2 + {u_3}^2}$

Inverses Element: $ q^{-1} = {q^* \over {| q |}^2} $

Darstellung eines Skalars s als Quaternion: $q = (s, 0)^T$

Darstellung eines Vektors v als Quaternion: $q = (0, v)^T$

Die Einbettung von SO(3) nach $\mathbb{H}$ nennt sich Einheitsquaternionen $\mathbb{S}^3$. Sie bilden folgende Gruppe: $\mathbb{S}^3 = { q \in \mathbb{H} \bigl| { | q | }^2 = 1 }$

Beweis über Gruppeneigenschaften:

Eine Gruppe ist ein Paar (G, ) bestehend aus einer Menge G und einer inneren zweistelligen Verknüpfung * auf G. $: G \times G \rightarrow G, (a, b) \rightarrow a * b$. Wenn die Verknüpfung folgende schwache Gruppenaxiome erfüllt, dann wird (G, * ) eine Gruppe genannt:

Es existiert ein linksneutrales Element $e \in G$, so dass gilt:

Für alle Gruppenelemente a gilt e * a = a
Zu jeden $a \in G $ existiert ein linksinverses Element $a^{-1} \in G$ mit $a^{-1} * a = e$

Rotation

Eine Rotation um eine Drehachse $\boldsymbol{a}$ mit $ | \boldsymbol{a} | = 1 $ und einem Drehwinkel $\phi$ kann wie folgt als Quaternion dargestellt werden: $q = ( cos {\phi \over 2} , \boldsymbol{a} sin { \phi \over 2} )$

Um die Rotation auf einen Vektor v anzuwenden, stellt man diesen als Quaternion dar und berechnet folgendes:

$v' = q v q^{-1}$

Weil q ein Einheitsquaternion ist, gilt $q^{-1} = q^{ * }$, daher können wir die Anwendung der Rotation auch wie folgt schreiben:

$v' = q v q^{ * }$

Verkettete Einheitsquaternionen q und r können zum Rotieren multipliziert werden: $q \cdot r$.

Interpolation

So wie man die Punkte auf einer Strecke zwischen zwei Punkten im Euklidischen Raum interpolieren kann, nutzt man auch einen Parameter $ t \in [0,1] $ um zwischen zwei Quaternionen zu interpolieren.

SLERP Interpolation (Spherical Linear Interpolation): $Slerp(\boldsymbol{q_1}, \boldsymbol{q_2}, t) = \boldsymbol{q_1} \cdot ( \boldsymbol{q_1}^{-1} \cdot \boldsymbol{q_2} )^t$ Das t ist eine Potenzierung und keine Transponierung.

Da das Potenzieren von Quaternionen nicht behandelt wird in der Vorlesung, gibt es eine direktere Formulierung der SLERP Interpolation:

$Slerp( \boldsymbol{q_1}, \boldsymbol{q_2}, t) = { sin(1-t) \theta \over sin \theta} \cdot \boldsymbol{q_1} + { sin t \theta \over sin \theta} \cdot \boldsymbol{q_2}$ Mit $ \langle \boldsymbol{q_1} | \boldsymbol{q_2} \rangle = cos \theta $

Mit dieser Formel erhält man eine konstante Winkelgeschwindigkeit.

Doppelte Abdeckung: Alle Orientierungen von SO(3), die in $\mathbb{H}$ als Einheitsquaternionen eingebettet sind, werden doppelt abgedeckt, das heißt, es gibt immer zwei Wege zu ihnen. $\boldsymbol{-q}$ und $\boldsymbol{q}$. Dass es sich um die gleiche Rotation handelt lässt sich über das Streichen von negativen Vorzeichen und der Konjugation zeigen.

=> SLERP berechnet nicht immer die kürzeste Rotation, d.h. man muss immer prüfen, welche kürzer ist.

Duale Quaternionen

Ersetze die vier reellen Werte der Quaternionen durch Dualzahlen, um Translationen ausdrücken zu können.

4. Vorlesung

(Tool Center Point, zum Beispiel Zentrum der Hand.)

Gelenktypen:

Rotationsgelenk R: Schulter
Torsionsgelenk T: Unterarmdrehung
Revolvergelenk V: Auch Schultergelenk bei passendem Winkel
Lineargelenk L (auch prismatic joint, Schubgelenk oder Translationsgelenk genannt)

R, T und V sind rotatorische Gelenke.

Arbeitsraum: Alle Punkte im Raum, die erreichbar sind -> in 3d sind mindestens 3 DoF nötig

Grundform des Arbeitsraumes: Arbeitsraum ohne Behinderung durch Roboterkörper oder gegenseitige Behinderung von Gelenken

Robotertypen:

Cartesian Robot
Cylindrical Robot
Kinematische Struktur
Spherical Robot
Articulated Robot
Parallel Robot, z. B. Stewart-Plattform für Autotests (6 DoF durch 3 rotatorische und 3 translatorisch)
Delta (Parallele Kinematik), z. B. bei selbstgebauten 3D-Druckern

Radkonfigurationen:

Differentialantrieb
Dreiradantrieb
Synchro-Drive
Mecanum-Antrieb (passive, zum Reifen tangentiale Rollen (45°) auf Reifen sorgen für geringere Reibung -> Bewegungen in alle Himmelsrichtungen, Armar3 und Armar6, KUKA)

Antriebe:

Fluidische Antriebe: Linearantrieb (Kolbenkraft, Kolbengeschwindigkeit, Drehmoment)
Muskelartige Antriebe: Pneomatisch (bei größeren Robotern durch Hydraulik ersetzen) (Hydraulik ist aber eigentlich nicht so präzise und schmierig in der Praxis -> Boston Dynamics benutzt aber für Atlas Hydraulik) Für Hände ist Pneumatik auch genutzt, weil es Platz für Sensoren in den kleinen Händen lässt. Man muss nur ein Ventil am Unterarm anbringen. (Armar3) Der Vorteil von Luft ist auch noch, dass sie nachgiebig ist und man daher auch zerbrechliche Sachen greifen kann
Elektrische Antriebe: Weniger Kraft, aber klein und schon elektrisch

Getriebe

Haben unterschiedliche Funktionen: Drehrichtung von Zahnrad wechseln, Achse wechseln, Umwandlung Drehmoment

Planetengetriebe: abhängig davon, wie viele Zahnräder und welche man fixiert. Antrieb, Abtrieb
Schneckenradgetrieben
Zahnstangengetriebe
Seilzug
Stirnradgetriebe
Schrauben und Spindelgetriebe: Formel dazu muss man nicht können
Harmonic Drive AG: Harmonic Drive Spannungswellengetriebe es können 1/3 bis 1/2 der Zähne im Angriff sein (aufeinanderliegen) -> viele kleien Zähne und wenig Spiel => Genauigkeit und sehr gute Umsetzung

Übersetzung

Kleinstes Zahnrad nennt sich Ritzel

5. VL = 1. Übung

Eulerwinkel aus SO(3)

Interessante Informationen aus der Besprechung des ersten Übungsblattes:

Wenn man aus einer kompletten Rotationsmatrix (z, x’, z’’): $R_{s} = R_{z}( \alpha ) \cdot R_{x’}( \beta ) \cdot R_{z’’}( \gamma )$ die Winkel herleiten möchte, dann kann man das entweder herleiten oder unter Annahme folgende Regeln verwenden:

$ \alpha = atan ( - {a_x \over a_y} ) $
$ \beta = acos ( a_z ) $
$ \gamma = atan ( {n_z \over o_z} ) $

Bedingung: $a_y \not= 0 $ und $ o_z \not= 0 $

SO(3) -> Quaternion

Wie kann man aus einer Rotationsmatrix R1 ein Quaternion berechnen, das die gleiche Rotation beschreibt.

$Rx = Ix \\ Rx - Ix = 0 \\ ( R-I ) \cdot x = 0 \\ ( R - \lambda I ) x = 0 \| \lambda = 1 \\$

Es handelt sich um ein Eigenwertproblem. Der Eigenvektor ist die Rotationsachse. -> LGS -> linear abhängige Terme

Drehwinkel: Zwei Varianten:

Rotation um orthogonalen Vektor
Spur: Wenn Rotationsachse normiert: $Spur(R(\alpha)) = 1 + 2 \cdot cos ( \alpha )$

6. Vorlesung

5.11.2018

Kinematisches Modell: Zusammenhänge zwischen Konfigurationsraum (Gelenke) und der Pose des Endeffektors im Arbeitsraum.

Welche Auswirkung hat nun eine Bewegung der kinematischen Kette? -> Kollision, Arbeitsraum

Vorwärtskinematik: Bestimmung der Lage des Endeffektors

Inverse Kinematik: Wie muss ich meine Gelenkwinkel verschieben, um in eine Pose zu kommen?

Gelenkwinkel $\theta_1 , … \theta_n$.

Direkte Kinematik: $X = f( \theta )$ mit X zum Beispiel aus $R^6: (x, y, t, \alpha, \beta, \gamma)$
Inverse Kinematik: $\theta = f^{-1}(X)$

Die Funktion $f$ muss aber nicht eindeutig umkehrbar sein.

Roboterarmbasis kann als Fixpunkt für kinematische Kette eines Armes interpretiert werden. Das wäre dann eine offene kinematische Kette, weil sie nur einen Fixpunkt hat. Wenn beide Enden fixiert sind, dann handelt es sich um eine geschlossene kinematische Kette.

Annahmen für die Berechnung der Pose des EEF:

Jedes Armelement ist ein Starrkörper
Jedes Gelenk hat nur einen Freiheitsgrad (Gegenbeispiel wäre ein Kugelgelenk)

Drehgelenke werden als Rolle dargestellt. Man kann sie auch kombinieren, um zum Beispiel eine Hüfte nachzuahmen.

Denavit-Hartenberg

Denavit-Hartenberg Konvention (in der Literatur nur DH) ermöglicht eine Translation und Rotation zwischen zwei Gelenkenkoordinatensystemen in einer kinematischen Kettte.

Wenn man mehrere solcher Denavit-Hartenberg-Transformationen verkettet, dann kann man unter Eingabe der Variablen (Drehwinkel…) eine kinematische Kette in der direkten Kinematik beschreiben.

Im Gegensatz zu einer homogenen Matrix oder (x,y,z,$\alpha$, $\beta$, $\gamma$) benötigt man nur 4 Parameter:

Armelementlänge a
Verwindung $\alpha$
Gelenkabstand d (Variable für Schubgelenke)
Gelenkwinkel $\theta$ (Variable für Drehgelenke)

Das heißt: $R^4 \rightarrow SE(3) \in R^{4x4}$, wobei man sagen muss, dass DH nicht den gesamten SE(3) abdeckt.

Für jedes Gelenk muss man auch ein “Offset” angeben, um die Null-Lage zu definieren.

Jacobi

Bei den Jacobi-Matrizen handelt es sich um das wichtigste Element für die Vorwärtskinematik und Inverse Kinematik. Mit ihr kann man Drehwinkelgeschwindigkeiten und Drehmomente in Gelenken berechnen. Beispiel: Ein Roboterarm soll 10kg tragen (Kraft am EEF), welche Drehmomente müssen die Antriebe leisten, damit es gehoben werden kann.

Beispiel Armar-1: $f: R^{n=7} \rightarrow R^{m=6}$, wobei f differentierbar sein muss.

[…]

7. Vorlesung

8.11.2018

8. Vorlesung

12.11.2018

9. Vorlesung

15.11.2018

10. Vorlesung

19.11.2018

Gastvortrag Stefan Schaale Google X

11. Vorlesung

22.11.2018

Wiederholung Lagrange-Methode

In der kinetischen Energie sind Gelenkwinkelgeschwindigkeit und translatorische Geschwindigkeit erhalten.

Bewegungsgleichung: $\tau_i = {d \over dt} ( { \partial L \over \partial \dot{q}_i } ) - { \partial L \over \partial q_i}$

Wobei $\tau_i$ generalisierte Kräfte (Drehmomente in den Gelenken) und $q_i$ generalisierte Koordinaten.

Bei Lagrange handelt es sich um ein geschlossenes Modell.

$E_kin$ und $E_pot$ für jedes Gelenk berechnen
Beide E in generaliserten Koordinaten ausdrücken: $L(q, \dot{q}) = E_kin(q, \dot(q)) - E_pot(q)$
Ableiten zum Lösen ($O(n^3)$)

Lagrange sagt aber nichts über Kräfte zwischen Segmenten (z. B. Oberarm zu Unterarm aus). Diese “Interaktionskräfte” nennt der Prof. Momente.

Die Herleitung aus der Arbeit eliminiert Momente oder externe Kraft durch Gewicht des zu hebenden Objektes -> Wechselwirkungen

Newton-Euler

Methode zur Modellierung der Dynamik ist linear $O(n)$, also gut berechenbar. Diese benutzt man auch wirklich!

Vorteile:

Beliebige Anzahl Gelenke
Belastung der Armelemente
O(n) -> echtzeitfähig
Rekursion

Es werden die Massenschwerpunkte $m_i$ der Segmente betrachtet. Darauf wirkt Kraft $F_i$ und dadurch Beschleunigung $\dot{v}_{s,i}$

Die Kraft entspricht dem Impuls abgeleitet nach Zeit (2. Gesetz Newton). $F_i = { d \over dt} (m_i v_{s,i}) = m_i \dot{v}_{s,i}$

Drehmoment enspricht Drehimpuls abgeleitet nach Zeit $N_i = {d \over dt} (I_i \dot{\omega}_{s,i})$

I steht hier für den Trägheitstensor. $\dot{v}$ ist eine translatorische Beschleunigung und $\dot{\omega}_{s,i}$ eine Winkelbeschleunigung.

Diese Beschleunigungen eines Armelements hängen von den Beschleunigungen der vorgehenden Armelementen ab. Dadurch kann man die Beschleunigungen von der Basis bis zum Endeffektor entlang der kinematischen Kette berechnen. -> Vorwärtsgleichungen

Die Kraft und Drehmomente eines Armelements hängen von den folgenden Armelementen ab. Man rechnet also vom Endeffektor zur Basis -> Rückwärtsgleichungen

Vorwärts

Ausgehend von den Ergebnissen der Kinematik $q$, $\dot{q}$ und $\ddot{q}$ werden folgende Werte bestimmt:

Winkelgeschwindigkeit $\omega_i$
Winkelbeschleunigung $\dot{\omega}_i$
Geschwindigkeit $v_i$ und Beschleunigung $\dot{v}_i$ der Basen der Koordinatensysteme
Geschwindigkeiten $v_{s,i}$ und Beschleunigungen $\dot{v}_{s,i}$ der Massenmittelpunkte der Armelemente

Man kann nun die Berechnung rekursiv formulieren, muss auch noch initialisieren.

Rückwärts

Man berechnet vom Greifer zu Basis mit den Ergebnissen aus der Vorwärtsgleichung.

Es werten dynamische Größen berechnet:

Auftretende Kraft $F_i$ im Schwerpunkt von Armelement i
Drehimpuls $N_i$ im Schwerpunkt von Armelem. i
Kraftvektor $f_i$, der von Armelem. i-1 auf i wirkt
Momentvektor $n_i$ vpm Armelem. i-1 auf i
Drehmoment skalar $\tau_i$ am Gelenk i

Kraft-Moment-Satz: $F = m a = m_i \cdot \dot{v}_i = f_i - f_i+1$

(Beschreibt Kräftegleichgewicht zwischen den Gelenken)

Drehimpulssatz:

$N_i = I_i \cdot \dot{\omega}_i = n_i - n_{i+1} + (-s_i - p_i) \times F_i - p_i \times f_i+1$

$p_i$ ist Länge Armelement und $s_i$ ist die Strecke vom folgenden Gelenk zum Massenschwerpunkt.

$\dot{\omega_i}$ und $\dot{v_i}$ stammt aus der Vorwärtsgleichung.

Und dann wieder rekursive Berechnung mit Initialisierung.

Herausf.

Herausforderungen Dynamik:

Nur Approximation der Dynamik
Es fehlen noch nicht-lineare Kräfte (z. B. Reibung), die nicht direkt modelliert werden können, aber ihr Einfluss ist auch nicht riesig Die nichtlinearen Effekte sind abhängig von Position, Geschwindigkeit und Beschleunigung
Dynamik ändert sich über die Zeit durch Abnutzung etc.
Dynamik ist abhängig von der Aufgabe, wenn Hammer in der Hand ist Modell anders

Wie geht man damit um? In der Automobilmontage hat man dafür sehr gute Modelle von allem und sehr präzise Greifer, zum Beispiel bei Windschutzscheibe.

Für humanoide Roboter muss man das lernen. Armar-6 hat 8 DoF pro Arm. Es wurden CAD-Modelle gemacht, aber es entstehen Ungewissheiten durch die Produktion. Das heißt, man sammelt Daten 6D-Pose beim Endeffektor und Messungen an Gelenken. Dadurch kann man ein datengetriebenes kinematisches Modell erstellen und benutzen ohne Visual-Servoing betreiben zu müssen.

Die Differenz zwischen Modell und Realität versucht man mit Maschinellem Lernen zu verringern.

Regelung

Jetzt haben wir Kinematik und Dynamik betrachtet, aber eigentlich wollen wir Bewegungen. Wir können wir dafür sorgen, dass unsere Vorgaben erreicht werden?

Regelungstechnik: selbsttätige, gezielte Beeinflussung dynamischer Prozesse während des Prozessablaufs.

Regelungstechnische Grundsituation: Auch wenn System nicht gut bekannt oder Störungen, Forderung nach selbsttätiger, gezielter Beeinflussung

Die Methoden der Regelungstechnik sind unabhängig vom System.

Aufbau einer Regelung (Die Regelung ist ein Wirkungskreislauf daher spricht man von Regelkreis)

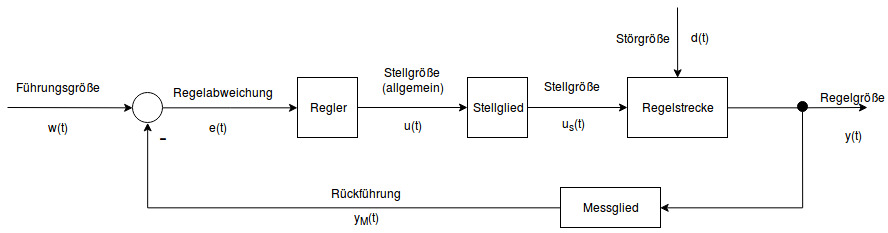
Die “Störgröße wird ausgeregelt”.

Die Norm DIN IEC 60050-351:2009-06 definiert den Begriff der Regelung wie folgt:

„Das Regeln, die Regelung, ist ein Vorgang, bei dem fortlaufend eine variable Größe, die Regelgröße, erfasst, mit einer anderen variablen Größe, der Führungsgröße, verglichen und im Sinne einer Angleichung an die Führungsgröße beeinflusst wird.
Anmerkung: Kennzeichen für das Regeln ist der geschlossene Wirkungsablauf, bei dem die Regelgröße im Wirkungsweg des Regelkreises fortlaufend sich selbst beeinflusst.“

Achtung: Regelung nicht mit Steuerung verwechseln. Bei der Steuerung gibt es aber keine Rückkopplung, das heißt auch kein geschlossener Wirkungskreislauf.

Im Englischen ist Regelung closed-loop control und Steuerung open-loop control.

Beispiel für Regelung: Drehzahlregelung eines Gleichstrommotors.

Laplace

Die Übertragungsglieder im Regelkreis ordnen dem Zeitverlauf der Eingangsgröße den Zeitverlauf der Ausgangsgröße zu.

Um Rechenvereinfachungen zu erhalten, stellen wir die Glieder nicht im Zeitbereich sondern im Laplace-Bereich dar. Das ist hilfreich unter der Annahme, dass wir Lineare zeitinvariante Systeme (LTI, siehe Grundlagen der Automatischen Spracherkennung) nutzen.

Die Übertragungsfunktion an einem Glied G wird dann wie folgt dargestellt:

$G(s) = {Y(s) \over U(s)}$

wobei die Großbuchstaben für die Laplace-Transformierte stehen. $s$ ist komplexe Frequenz.

Laplace-Transformation:

$L\{f(t)\} = F(s) = \int_{0}^{+ \infty } f(t) e^{-st} dt$ wobei f(t) das Signal und s komplexe Zahl ($ s := \sigma + j\omega$ ). Für alle negativen t ist f(t)=0.

LP-Transformierte: $L\{a\} = ... = a/s$

$f(t) = t F(t) = 1/s^2$

12. Vorlesung

26.11.2018

Übungsblatt 3

Jacobi-Matrix invertieren

Regel von Sarrus

Singularitäten Eine kinematische Kette ist in einer singulären Konfiguration, wenn seine Jacobi nicht vollen Rang hat. Bei quadratischer Matrix A: wenn det(A) = 0 -> Singularitäten

Auch wenn am Ende zwei parametrische Lösungen herauskommen, sind es unendlich viele Singularitäten, die möglich sind, auch wenn Winkel periodisch.

Dynamikmodellierung mit Lagrange

13. Vorlesung

29.11.2018

Laplace

LPTF: $L\{ f(t) \} = F(t) = \int_{0}^{\infty}{ f(t) e^{-st} dt }$

$L \{ { t^{k-1} \over (k-1)! } \} = {1 \over s^k }$

LPTF Ableitungsfunktion:

$L\{ \dot{f}(t) \} = s \cdot F(s) - f(0)$

LPTF Integral:

$f(t) = \int_0^{t} f(\tau) d\tau F(T) = 1/s F(s)$

LPTF exp:

$L\{ e^{-\alpha t} \} = {1 \over s + \alpha}$

Dirac-Stoß: $\delta(t) = \infty$, wenn t=0, 0 sonst.

Einheitssprung: $\sigma(t) = 1$, wenn t >= 0, 0 sonst

L{$\delta$} = 1

L{$\sigma(t)$} = $e^{-\delta t} \cdot (cos \omega t - j sin \omega t)$ Dabei handelt es sich um die komplexe Darstellung einer Schwingung für die gilt:

$\delta > 0 \to 0$ Schwingung klingt ab
$\delta = 0 \to 1$ Dauerschwingung
$\delta < 0 \to - \infty $ Schwingung klingt auf

Transf. Regeln

Linearität: $L{ \alpha f_1(t) + \beta f_2(t) } = \alpha F_1 (s) + \beta F_2 (s) $
Faltungssatz: $L { f_1(t) * f_2(t)} = F_1(s) \cdot F_2(s)$
Grenzwertsatz: $f_1(t=0) = \lim_{s \to \infty} s * F(s) $
Differentiationssatz: $ L { { d \over dt } f(t) } = s F(s) $
Integrationssatz: $ L { \int f(t) dt } = {1 /over s} F(s) $
Verschiebung: $ L { f(t - \tau) } = e^{-\tau s} F(s) $
$L{ e^{\alpha t} = { 1 \over s - \alpha} }$
$ L{t^n} = { t! \over s^{n+1} } $ für n = 1,2,…
$ L { sin(\alpha t) } = \alpha \over {s^2 + \alpha^2} $
$ L { cos(\alpha t) } = s \over {s^2 + \alpha^2} $

Übertragungsglieder

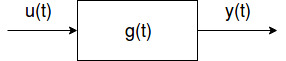
Wir betrachten hier ein LZI (Lineares zeitinvariantes) Übertragungsglied. LZI-Glied: y(t) = g(u(t)) Das ist dann im Zeitbereich eine Faltung: $y(t) = g(t) * u(t)$

Welche zum Rechnen in den komplexen s-Bereich transformiert wird:

Y(t) = G(t) \cdot U(t)

P

Proportionalglied P-Glied

$y(t) = K u(t)$

P-Glied

I

Integrierglied

$y(t) = \int_{0}^{\tau}{u(\tau) d\tau}$

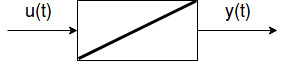
I-Glied

Laplace-Transformierte: $Y(s) = K \cdot {1 \over s} \cdot U(s) = {K \over s} \cdot U(s) \rightarrow G(s) = { K \over s }$

Wenn: $u(t) = \sigma (t)$ Eingangssignal also Einheitssprung LPTF: $ U(s) = 1 \over s $

$ Y(s) = { K \over s } \cdot { 1 \over s} = K \over s^2 $ => Rücktransformation weil $LP^{-1} {1 \over s^2} = t$ => $ y(t) = K \cdot t $

D

Differenzierglied

$y(t) = K \cdot \dot{u}(t)$

D-Glied

T

Totzeit Glied

$T_t$-Glied

$y(t) = K \cdot u(t - T_t)$

T-Glied

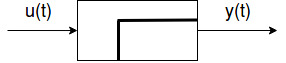
S

Summenglied. Als Kreis.

KL

Kennlinienglied

y(t) = K f(u(t))

M

Multiplizierglied

$ y(t) = K \cdot u_1 (t) u_2 (t) $

Vorsteuerung

Wenn man eine Geschwindigkeitsregelung mit einem P-Regler betrachtet, dann ergibt sich folgendes Problem: Man möchte einen gewissen Winkel erreichen, macht aber Geschwindigkeitsvorgaben. Das heißt, wenn die Geschwindigkeitsvorgabe erreicht wurde, dann ist die Regelabweichung Null und dadurch wird auch die Stellgröße Null.

Diesem Problem begegnet man mit Hilfe einer Vorsteuerung.

Wikipedia dazu:

Die Vorsteuerung bezeichnet ein Element des Reglerentwurfs, das die Stellgröße mit einem Wert beaufschlagt, der unabhängig von den Zuständen der Regelstrecke und daraus resultierenden Messungen ist. Die Vorsteuerung ermöglicht die Berücksichtigung des aufgrund des Sollwertverlaufs zu erwartenden Stellgrößen-Bedarfs. Da sie eine Steuerung ist, kann sie das Führungsverhalten verbessern ohne die Stabilität zu gefährden. Analog können auch gemessene Störgrößen aufgeschaltet werden. In diesem Fall spricht man von Störgrößenaufschaltung.

PID

Ein PID-Regler besteht aus einem P-, I- und D-Glied.

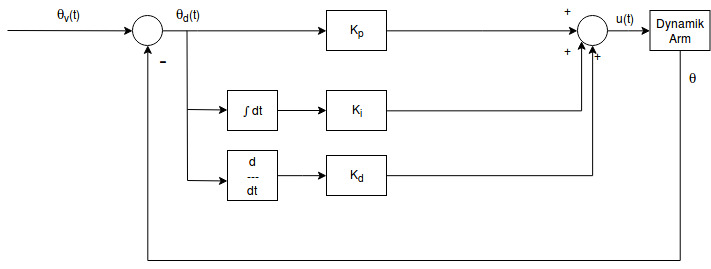
PID-Regler

$u(d) = \tau = K_p \theta_d + K_i \int \theta_d (t) dt + K_d \dot{\theta}_d$

Aufgaben:

Kp ist eine “virtuelle Feder”, den Positionsfehler minimiert
Kd ist ein “virtueller Dämpfer”, der Geschwindigkeitsfehler minimiert
Ki reduziert die Regelabweichung (Offsets)

$ L{ \tau } $ -> Übertragungsfunktion $G(s) = K_p + K_I {1 \over s} + K_{D} s $

Wenn weder Regler noch Strecke kein I-Verhalten haben, dann wird Offset nie reduziert. Gleichstrommotor hat es aber.

Stabilität

Stabilität einer Regelung. Vergleiche komplexe Schwingung mit $\delta > 0$. Bei PID wenn $K_p$ zu groß.

Ziel ist ein stabiles System, bei dem mit der Zeit die Regelabweichung gegen Null geht.

Wie finden?

DGL aufstellen und mit Laplace-Transformation lösen, dann Nullstellen suchen.

Testfunktion

Antwort eines Systems auf Testfunktionen:

Impulsfunktion
Sprungfunktion
Anstiegsfunktion
Harmonische Funktion

Bei humanoiden Robotern benötigen wir für die Regelung die Inverse Kinematik, um eine “kartesische Regelung” zu ermöglichen, da wir die Zielvorgaben ja nicht im Gelenkwinkelraum machen wollen.

“98% der Instustrieroboter werden Positionsgeregelt. Erst in letzter Zeit Drehmoment- und Kraftregelung”.

Wenn die IK in Regelung enthalten, dann hat man höheren Rechenaufwand.